Damped LC tank with external excitation
We consider a resistor, an inductance and a cap in series excited by an external AC signal.
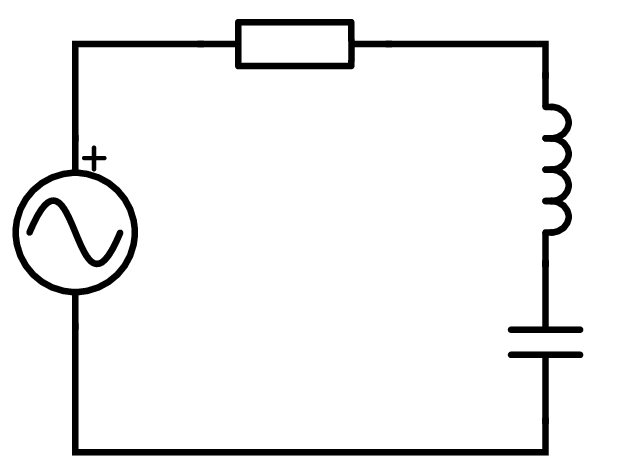 |
This circuit is mathematically described by
 | |
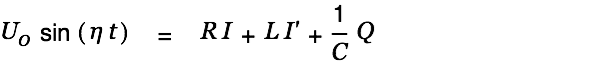 | |
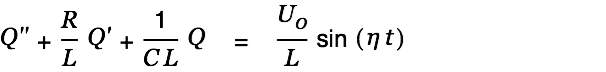 | (1) |
Solving the homogeneous part of the differential equation
We solve the homogeneous part of the differential equation Eq. 1 first
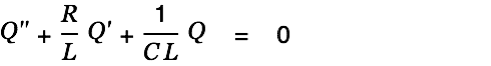 | (2) |
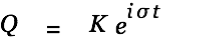 | |
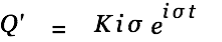 | |
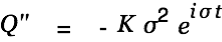 |
Substitution into the differential equation gives
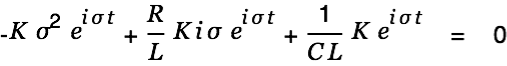 | |
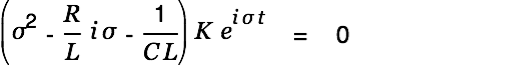 |
This equation is true for all
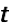 only if
only if
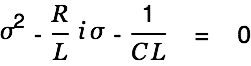 |
is true. We solve this as follows:
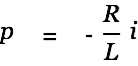 | |
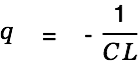 |
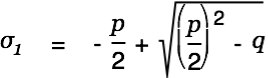 | |
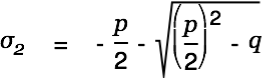 |
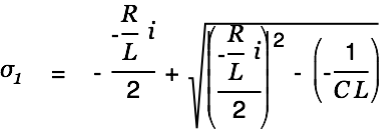 | |
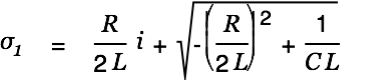 | |
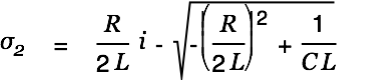 |
We define
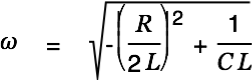 |
 | |
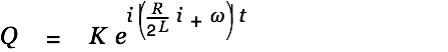 | |
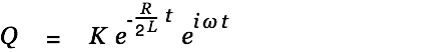 | |
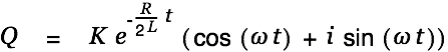 |
 | |
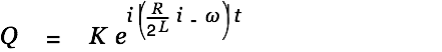 | |
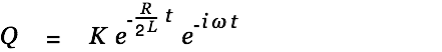 | |
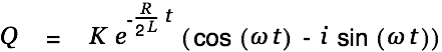 |
The general solution for the homogeneous differential equation can therefore be written as
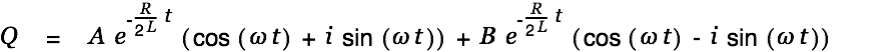 | |
 | |
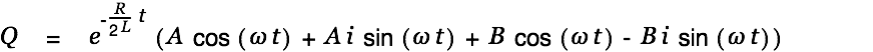 | |
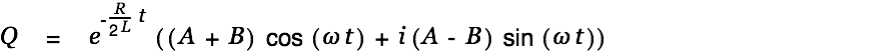 |
or after replacing the factors
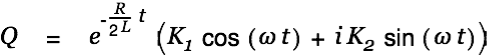 |
Since the differential equation is linear we can rewrite this as follows
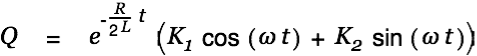 |
or even shorter like so
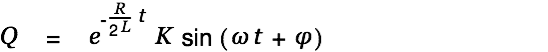 | (3) |
 | (4) |
 | (5) |
 | (6) |
with the two freely choosable constants
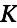 und
und 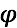 . Please note the dependence of the resonance frequency from the resistance.
. Please note the dependence of the resonance frequency from the resistance.
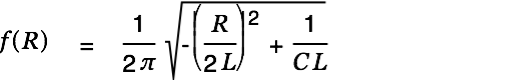 | (7) |
 |
Finding a particular solution for the inhomogeneous differential equation
We find a particular solution for the inhomogeneous differential equation by trying a suitable approach.
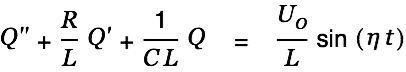 |
A suitable approach for the above equation is
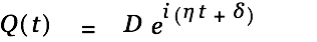 | |
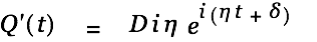 | |
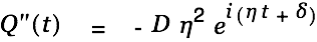 |
Substituted into the differential equation we get
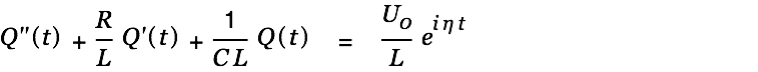 | |
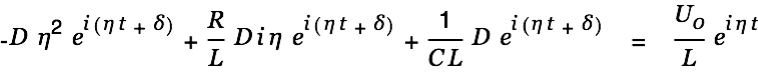 | |
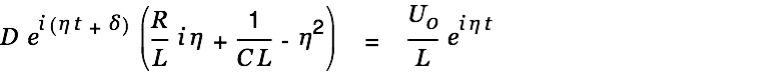 | |
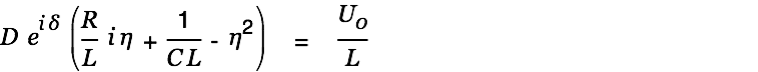 |
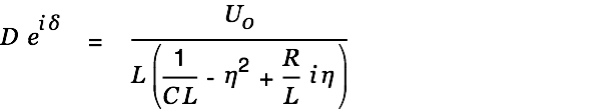 | |
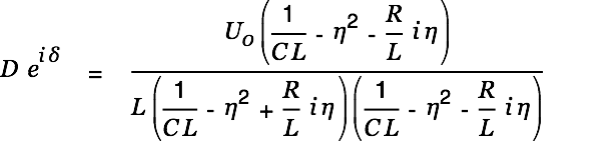 | |
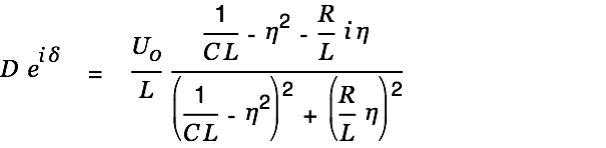 | |
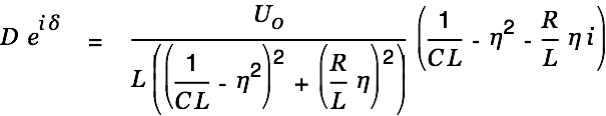 |
The value
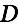 is the length of the complex number on the right.
is the length of the complex number on the right.
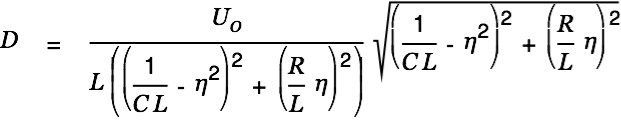 | |
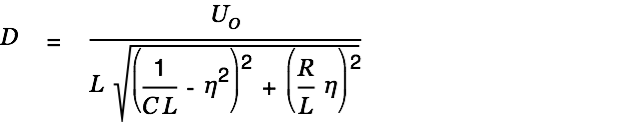 |
The angle
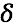 is determined as follows:
is determined as follows:
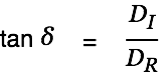 | |
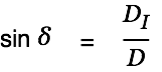 | |
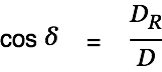 |
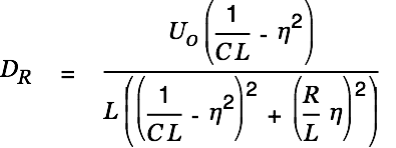 | |
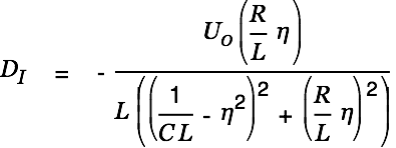 | |
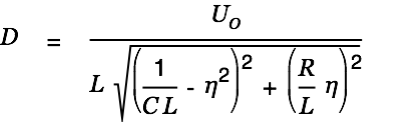 |
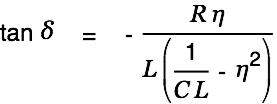 | |
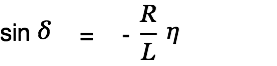 | |
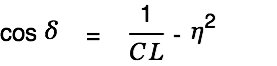 |
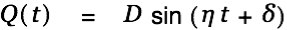 |
Combining the general and the particular solution
We combine the general solution for the homogeneous differential equation
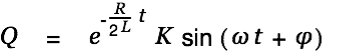 | |
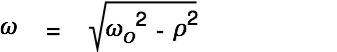 | |
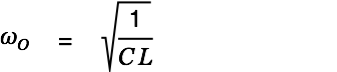 | |
 |
and the particular solution of the inhomogeneous differential equation
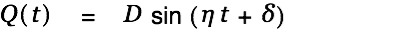 | |
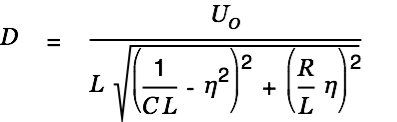 | |
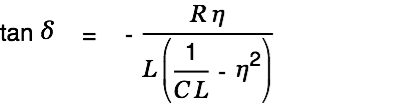 |
into a total solution by summation:
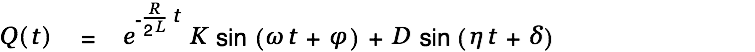 | (8) |
Since the e-Function approaches 0 for large values of
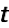 only the particular solution remains after an initiation period.
only the particular solution remains after an initiation period.
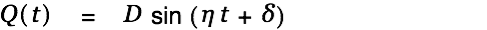 | (9) |
We devide by
 to get the voltage in the cap, take first derivatives to get the current and take the second derivative to get the voltage over the coil.
to get the voltage in the cap, take first derivatives to get the current and take the second derivative to get the voltage over the coil.
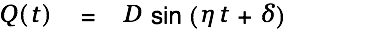 | |
 | |
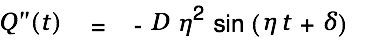 | |
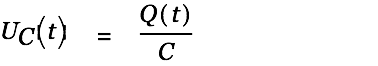 | |
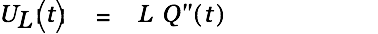 | |
 | |
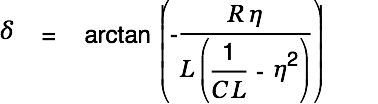 |
 |
We determine the peak voltage in the cap and the peak current with respect to
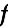 (resonance frequency):
(resonance frequency):
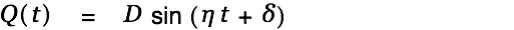 | |
 | |
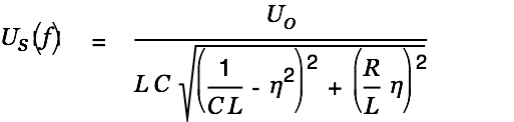 | |
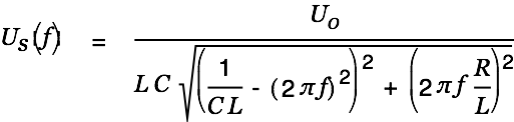 |
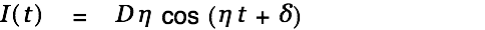 | |
 | |
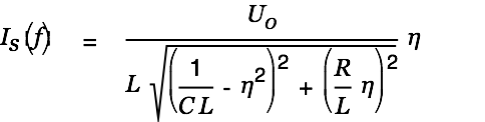 | |
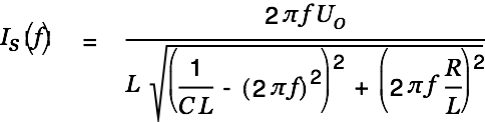 |
 |
If we excite the series tank with its resonance frequency we get high voltages over the components and a very high current only limited by the resistance of the wire.
Energy Consideration
The power going into the circuit is given by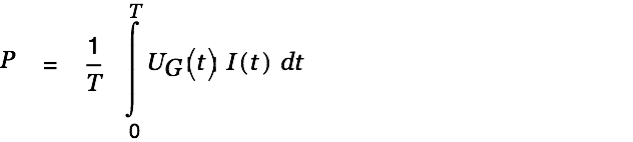 | |
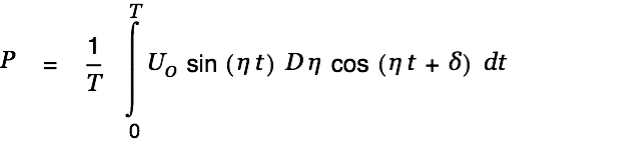 | |
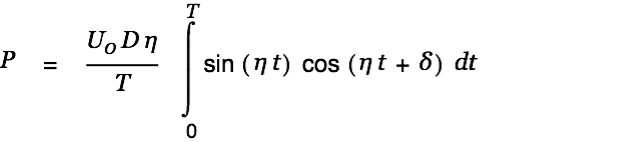 | |
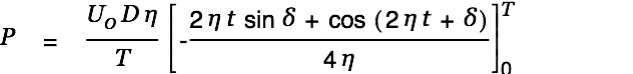 | |
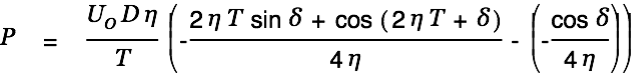 | |
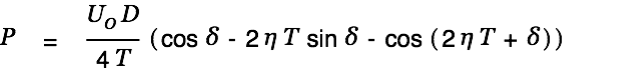 | |
 | |
 |
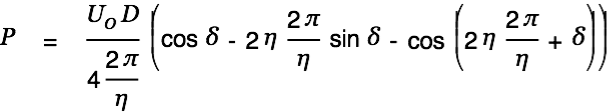 |
This gets us the following expression for the input power.
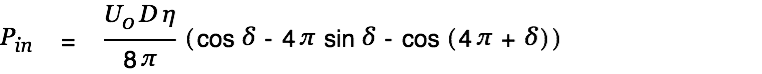 | (10) |
 | |
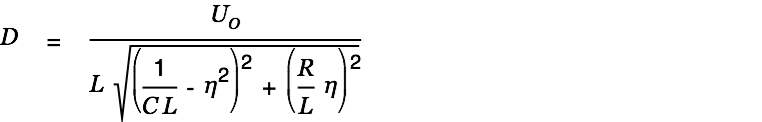 |
The circulating power in the circuit is defined as
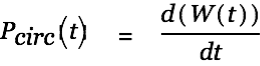 |
with
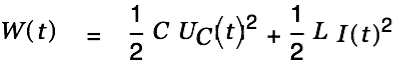 |
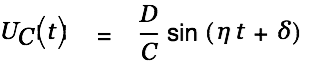 | |
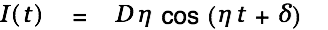 |
 | |
 | |
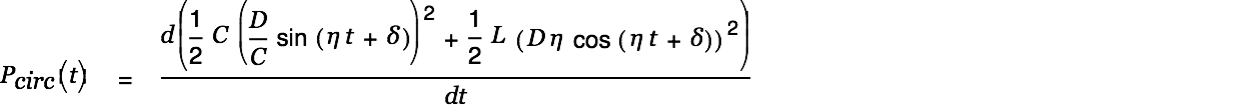 | |
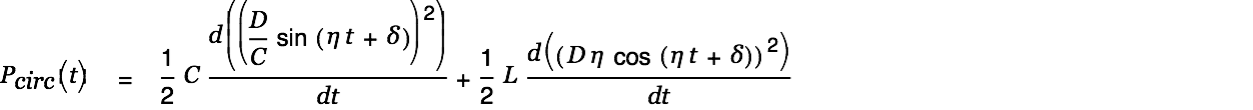 | |
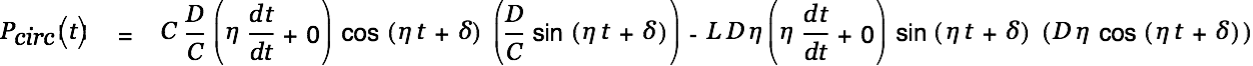 | |
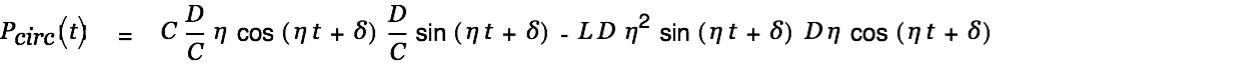 | |
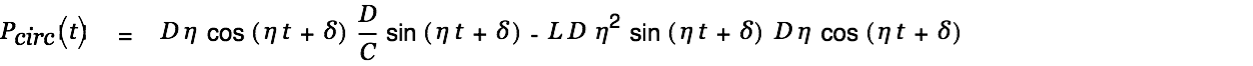 | |
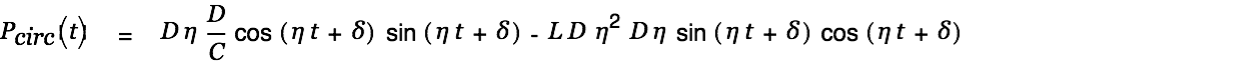 | |
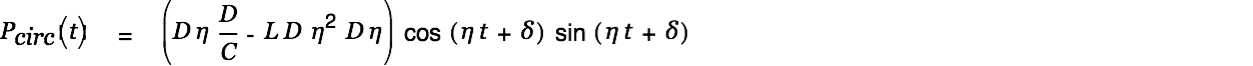 | |
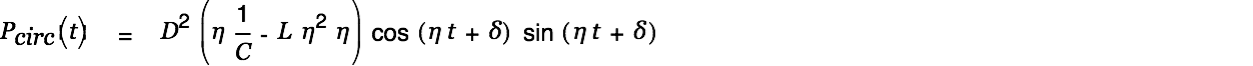 | |
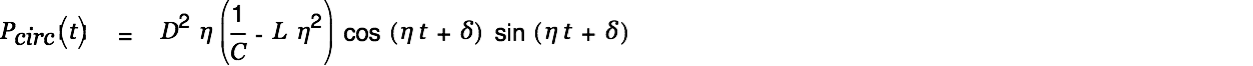 | |
 | |
 |
 |
We have scaled
 with a factor of 100 in the figure above. The Input power is very small compared to the circulating power for
with a factor of 100 in the figure above. The Input power is very small compared to the circulating power for 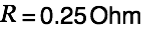 .
.News
| 23.04.2023 | Cassiopeia 2.9.0 released |
| 05.10.2022 | Cassiopeia 2.8.3 released |
| 29.09.2022 | Cassiopeia 2.8.0 released |
| 08.07.2022 | Cassiopeia 2.7.0 released |
| 14.04.2021 | Cassiopeia 2.6.5 released |
| 10.02.2021 | Cassiopeia 2.6.1 released |
| 26.06.2015 | Word Processor Comparison |
| 24.06.2015 | Updated Documentation |
| 23.06.2015 | Cassiopeia Yahoo Group |
| 18.06.2015 | Advanced Data Security |
| 11.05.2015 | Cassiopeia Overview |
| 08.05.2015 | Exporting to files |
| 14.05.2013 | LaTeX and HTML Generation |
| 08.05.2013 | Example Paper released |
| 26.04.2013 | Co-editing in a workgroup |
| 16.04.2013 | Equation Editor Quick Reference |
| 12.04.2013 | Equation Editor |
| 04.04.2013 | Links and Bibliography |
| 01.04.2013 | Books |
| 30.03.2013 | Documents |
| 28.03.2013 | Simulations |
| 16.03.2013 | 2D Graphs |
| 10.03.2013 | Symbolic Algebra |
| 08.03.2013 | Getting Started |
| 07.03.2013 | Installation and Setup |
White Papers
| 13.10.2015 | 01 Writing documents |
| 15.10.2015 | 02 Using the equation editor |
Youtube
| 08.07.2022 | Installation & Getting Started |
| 14.04.2021 | Animating Wave Functions |
| 26.01.2016 | Keystroke Navigation |
| 22.10.2015 | Equation Editor Demo |
| 19.06.2015 | Equation Editor Tutorial |
| 10.06.2015 | Sections and Equations |
| 09.06.2015 | Getting Started |
| 09.06.2015 | Damped Oscillations |
| 29.05.2015 | Solving equations |
| 13.05.2015 | Privileges and Links |
| 19.06.2013 | Magnetic Field |
| 14.06.2013 | Creating Documents |
| 10.06.2013 | Vector Algebra |
| 30.05.2013 | Differential Simulations |
Contact
Smartsoft GmbH Advanced Science Subdiv.Support: support@advanced-science.com

