Symbolic Algebra
Cassiopeia uses MathML content markup to represent equations internally. Equations thus have mathematical meaning and can therefore be processed by the built-in symbolic algebra system.
Taking derivatives
Press Command-y to create a new equation and then type "y", "=", "a", Ctrl-l, "3", <Cursor-up>, <Cursor-right>, "x", Ctrl-h, "3", <Cursor-up>, <Cursor-right>, "+", "a", Ctrl-l, "2", <Cursor-up>, <Cursor-right>, "x", Ctrl-h, "2", ...
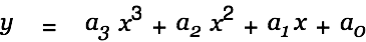 |
Now Command-Shift-Doubleclick on this equation to open the equation inspector
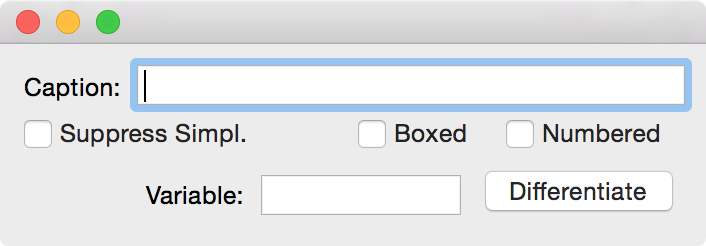 |
enter x in the Variable field and click on Differentiate. The following equation is generated automatically.
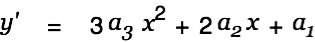 |
Repeating this process gives
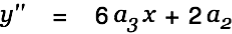 |
That's one way of taking derivatives. There is another one. Create a new equation with Command-y and then type "z", "=", Ctrl-d
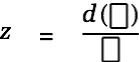 |
Insert an "y" in the enumerator cell and "d", "x" in the denominator cell.
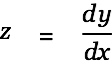 |
Now Alt-Drag the first equation onto the last one. Cassiopeia creates a copy of the last equation and inserts the dropped one, replacing the y in the enumerator with the right side of the dropped equation.
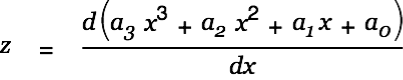 |
Now Alt-Doubleclick on the last equation to simplify. Do this a couple of times until you get the desired result.
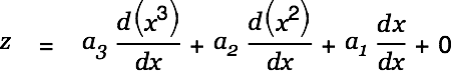 | |
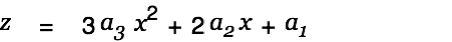 |
In the above example we had to explicitly specify a derivation variable. This would not have been necessary if we entered a function instead of an equation. A function requires the specification of a function variable. Create a copy of the function above (just doubleclick on it), then click into the equation and remove the y on the left of the equal sign. Then type "y", "(", "x", ")". The equation should look as follows now.
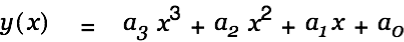 |
We have defined a function. Open the equation inspector with Command-Shift-Doubleclick on this formula. It is now no longer necessary to explicitly specify a derivation variable. Just click on Differentiate to take the derivative of the function.
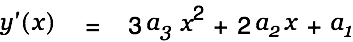 |
Do this again to get the second derivative.
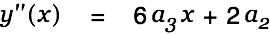 |
Being precise - specifying a function variable on the left side - has made the explicit specification of a derviation variable superfluous. Moreover, since Cassiopeia can recognize the functional character of this equation now it can be drawn without further ado. Shift-doubleclick on the equation or alternatively choose SDM - FunctionGrapfh2D from the menu and drag the function onto the textview of the appearing function graph inspector.
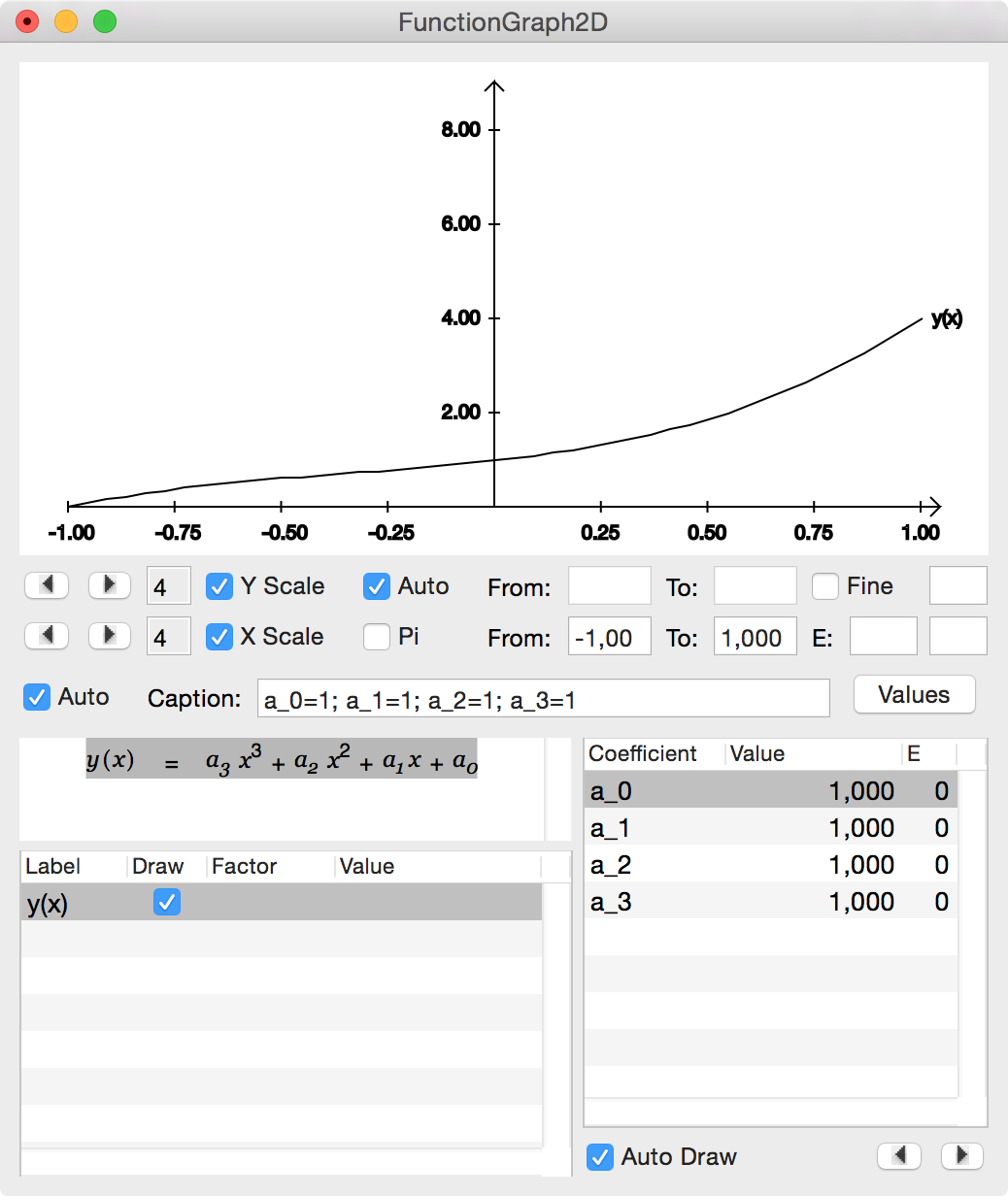 |
The graph plot is inserted into the document below the shift-doubleclicked function. Drag the other two functions y' and y'' from the document into the textview on the 2D graph inspector and change the from value to 0. Press <Enter> after modifying a value to trigger redraw.
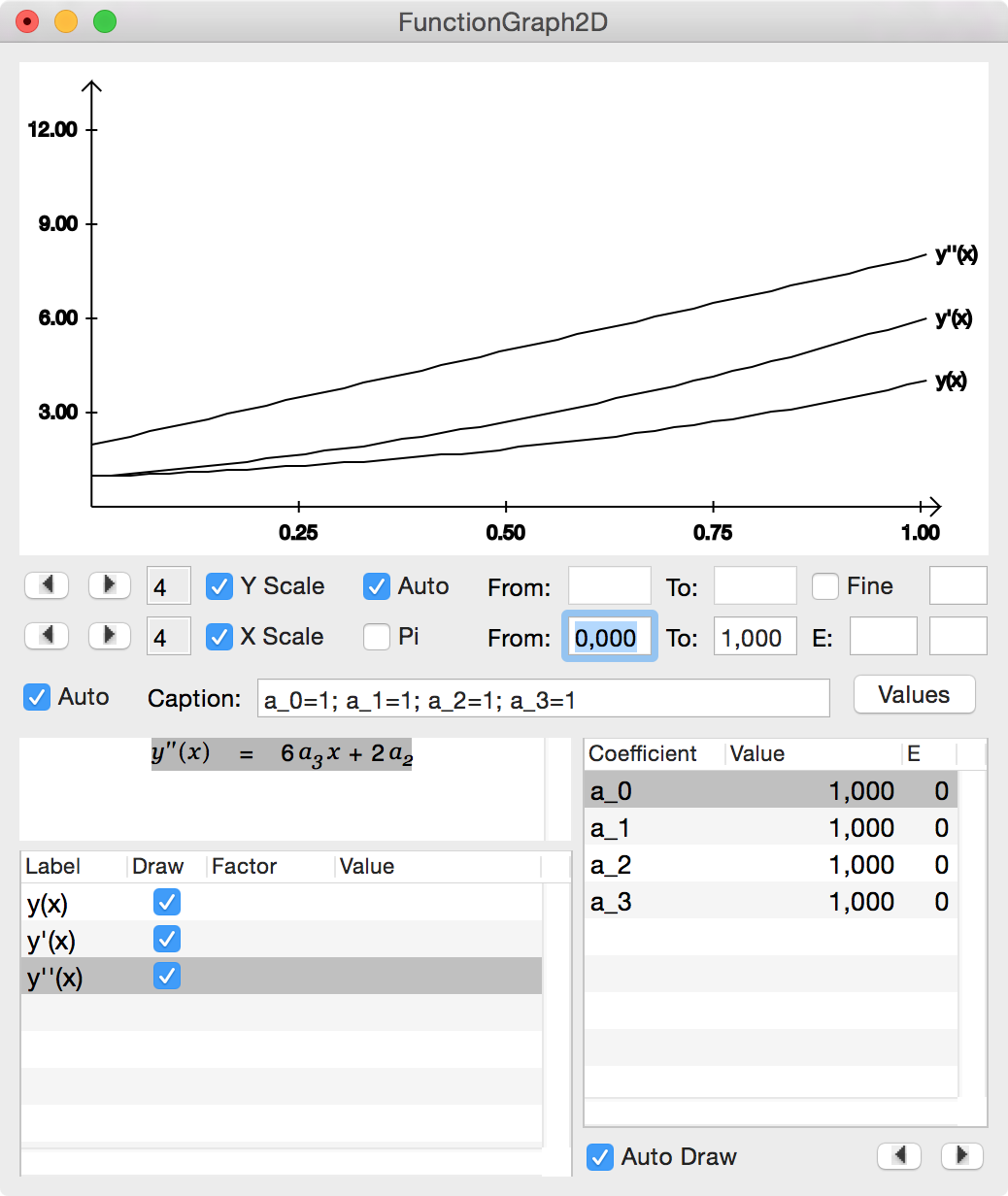 |
Play with the x and y limits until your are satisfied with the graph. Then choose Tools - Colors from the Cassiopeia menu, select colors and drag one color on each of the three functions in the tableview.
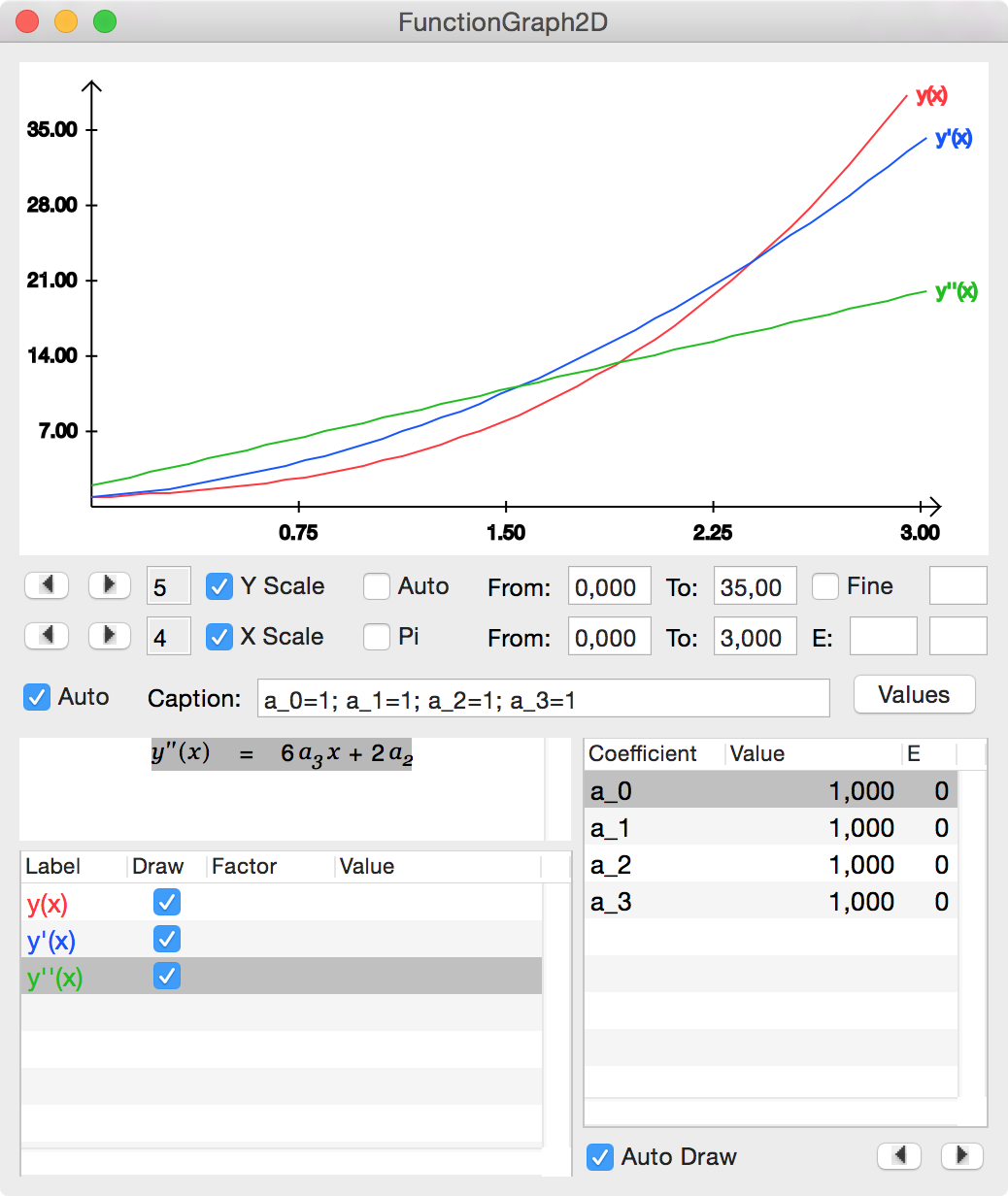 |
You might also want to play with the values of the coefficients. Generate a PDF for your document. You should get something like the following:
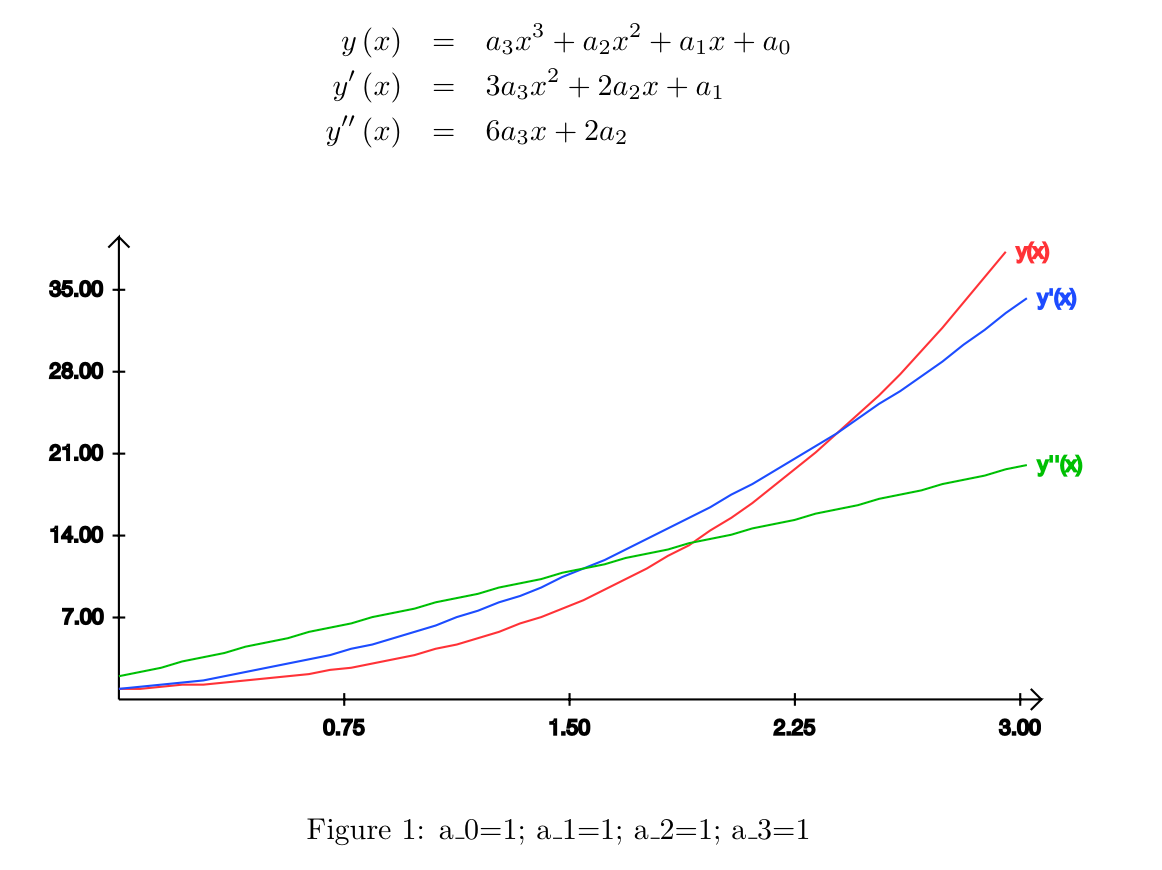 |
Solving Integrals
We want to solve a few integrals now using the integrated symbolic algebra system. Assume you want to calculate the volume of a sphere. Create a new equation with Command-y and type in the infinitesimal volume element in spherical coordinates like so "d", "V", "=", "r", Ctrl-h, "2", <Cursor-up>, <Cursor-right>, "s", "i", "n", Ctrl-g "b", <Cursor-up>, <Cursor-right, "d", Ctrl-g "b", "d", Ctrl-g "a", d, "r", <Return>
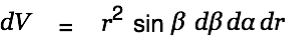 |
Then in a new equation write down the integral like so: "V", "=", Ctrl-i "d", "d", "V"
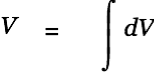 |
then Alt-drag the infinitesimal volume element onto this equation. dV is replaced with its assignment.
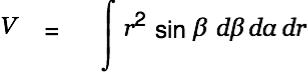 |
Alt-Doubleclick on this equation. Cassiopeia detects multiple d... terms and expands the equation to the following form.
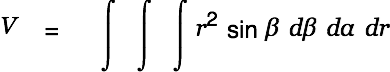 |
Now click into the center of this equation and hit <Cursor-up> until the inner integral is selected.
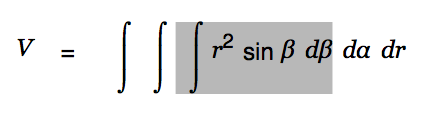 |
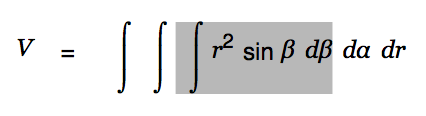 |
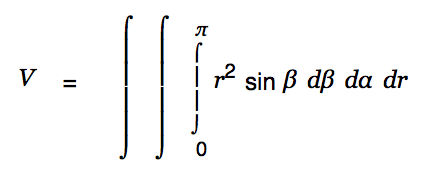 |
Press <Cursor-up> until the middle integral is selected
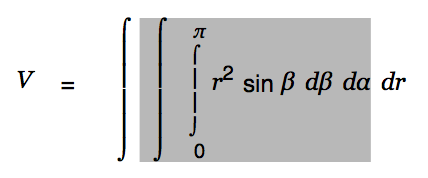 |
and hit Ctrl-y to upgrade that integral as well.
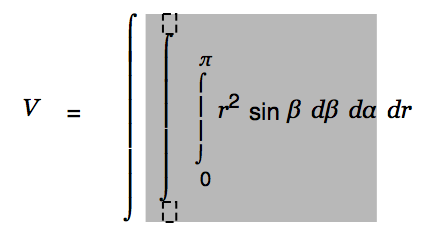 |
Enter "0" for the lower limit and "2", Ctrl-g p for the upper limit.
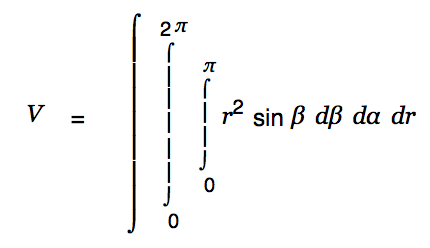 |
Press <Cursor-up> until the outer integral is selected. Upgrade that as well and set the limits 0 and R.
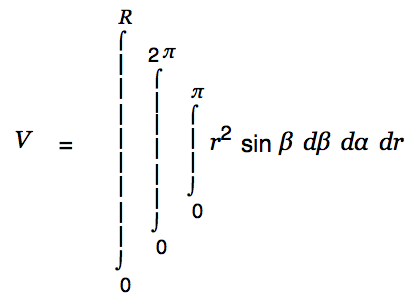 |
We are done with the creative part. Cassiopeia can handle the rest of the work. Just Alt-doubleclick on the equation(s) until the result is presented as shown below.
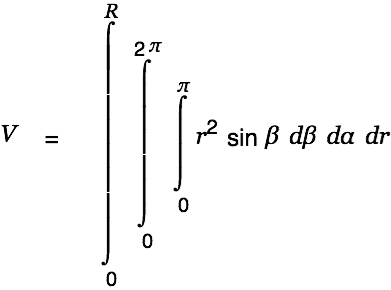 | |
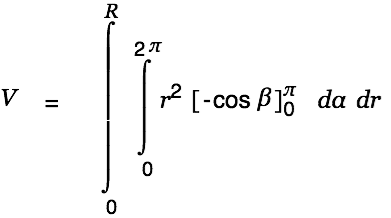 | |
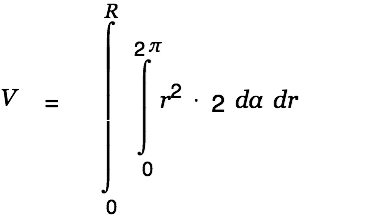 | |
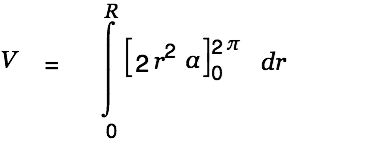 | |
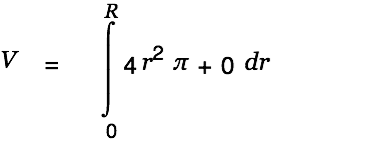 | |
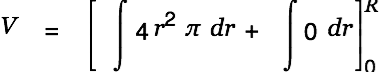 | |
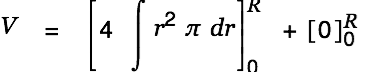 | |
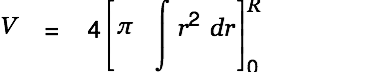 | |
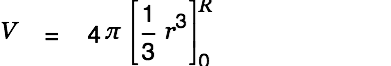 | |
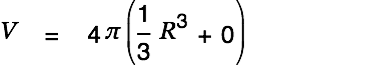 | |
 |
We have started the above integration with a dintegral (Ctrl-i d). A dintegral has a single cell behind the integral sign and is useful for expressions of the form
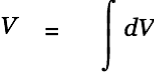 |
This is a rather special case. In most other cases we would probably rather like to start with the normal integral part reachable via Ctrl-i i. Create a new equation, then type "y", "=", Ctrl-i i.
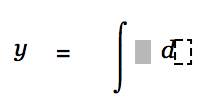 |
Note that this integral part has two cells, one for the integrand and one for the differential. Fill the body of the integral with "3", "x", Ctrl-h, "3", use the cursor keys to move to the differential cell and type "x".
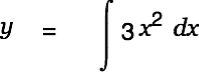 |
Alt-Doubleclick on this equation. This gets us
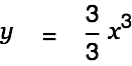 | |
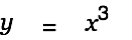 |
News
| 23.04.2023 | Cassiopeia 2.9.0 released |
| 05.10.2022 | Cassiopeia 2.8.3 released |
| 29.09.2022 | Cassiopeia 2.8.0 released |
| 08.07.2022 | Cassiopeia 2.7.0 released |
| 14.04.2021 | Cassiopeia 2.6.5 released |
| 10.02.2021 | Cassiopeia 2.6.1 released |
| 26.06.2015 | Word Processor Comparison |
| 24.06.2015 | Updated Documentation |
| 23.06.2015 | Cassiopeia Yahoo Group |
| 18.06.2015 | Advanced Data Security |
| 11.05.2015 | Cassiopeia Overview |
| 08.05.2015 | Exporting to files |
| 14.05.2013 | LaTeX and HTML Generation |
| 08.05.2013 | Example Paper released |
| 26.04.2013 | Co-editing in a workgroup |
| 16.04.2013 | Equation Editor Quick Reference |
| 12.04.2013 | Equation Editor |
| 04.04.2013 | Links and Bibliography |
| 01.04.2013 | Books |
| 30.03.2013 | Documents |
| 28.03.2013 | Simulations |
| 16.03.2013 | 2D Graphs |
| 10.03.2013 | Symbolic Algebra |
| 08.03.2013 | Getting Started |
| 07.03.2013 | Installation and Setup |
White Papers
| 13.10.2015 | 01 Writing documents |
| 15.10.2015 | 02 Using the equation editor |
Youtube
| 08.07.2022 | Installation & Getting Started |
| 14.04.2021 | Animating Wave Functions |
| 26.01.2016 | Keystroke Navigation |
| 22.10.2015 | Equation Editor Demo |
| 19.06.2015 | Equation Editor Tutorial |
| 10.06.2015 | Sections and Equations |
| 09.06.2015 | Getting Started |
| 09.06.2015 | Damped Oscillations |
| 29.05.2015 | Solving equations |
| 13.05.2015 | Privileges and Links |
| 19.06.2013 | Magnetic Field |
| 14.06.2013 | Creating Documents |
| 10.06.2013 | Vector Algebra |
| 30.05.2013 | Differential Simulations |
Contact
Smartsoft GmbH Advanced Science Subdiv.Support: support@advanced-science.com

