Energy transfer from one capacitor to another
It was suggested to extract power from a generator coil into a fist cap, to disconnect this cap from the generator coil and connect it to a second cap, then disconnect the second cap from the first and pump the charge of the second cap into a load.
 |
We assume a voltage 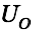 in
in 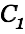 and no voltage in
and no voltage in 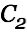 at
at 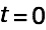 . The switch between the two caps is closed allowing current to flow from the first to the second capacitor.
. The switch between the two caps is closed allowing current to flow from the first to the second capacitor.
 | |
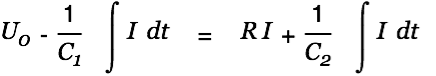 | |
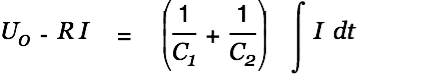 | |
 | |
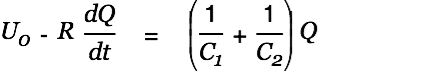 |
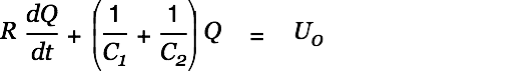 | (1) |
We first solve the homogeneous part of this differential equation with the following approach:
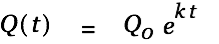 | |
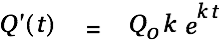 |
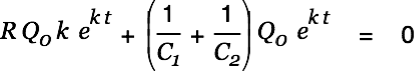 | |
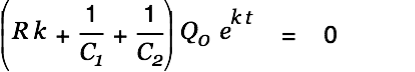 |
This is true for all
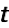 only if
only if
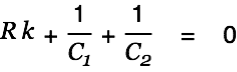 |
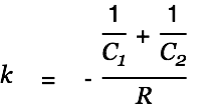 | |
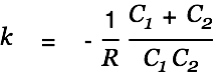 |
A solution for the homogeneous differential equation is therefore
 | (2) |
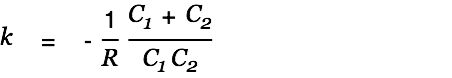 | (3) |
We find a solution of the inhomogeneous differential equation by varying the factor.
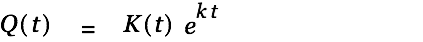 | (4) |
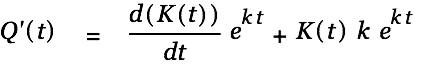 |
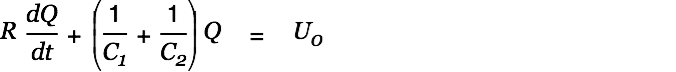 | |
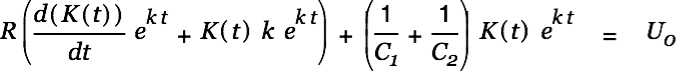 | |
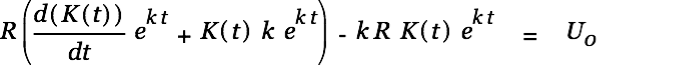 | |
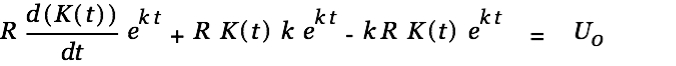 | |
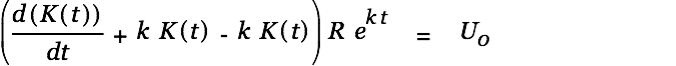 |
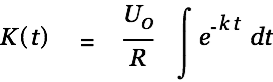 | |
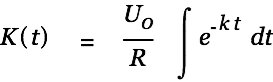 | |
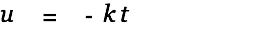 | |
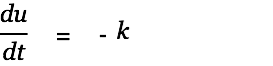 |
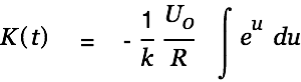 | |
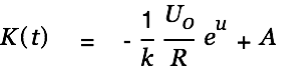 |
We substitute this result into Eq. 4
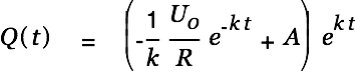 |
and thus get a particular solution for the inhomogenous differential equation Eq. 1:
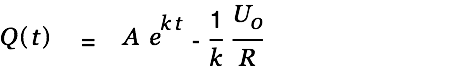 | (5) |
Since
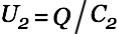 we have
we have
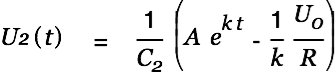 |
If we assume
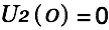
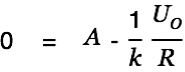 | |
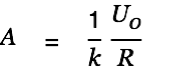 |
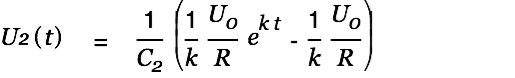 | |
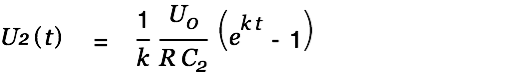 | (6) |
We substitute
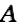 into Eq. 5 and get
into Eq. 5 and get
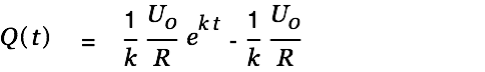 | |
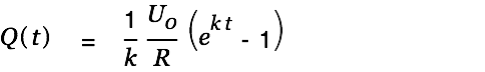 | (7) |
We get the current by taking the derivative of Eq. 7:
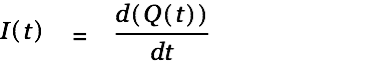 | |
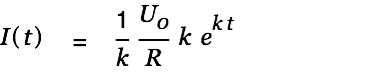 | |
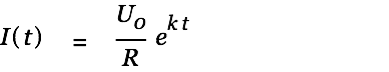 | (8) |
The voltage in the source cap is given by
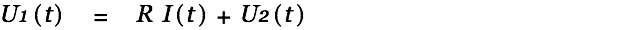 | |
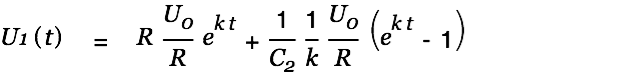 | |
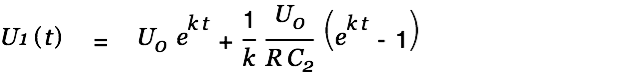 | (9) |
We plot these three functions.
 |
We have
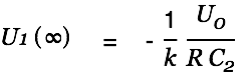 | |
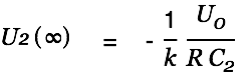 | |
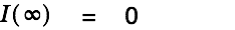 |
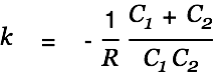 |
Energy Consideration
The initial energy in the system is given by
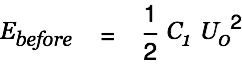 |
The energy after the charge transfer is given by
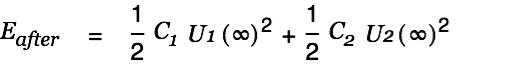 | |
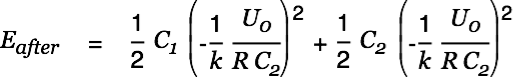 | |
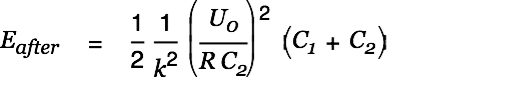 | |
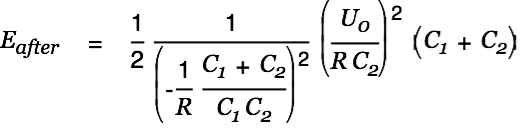 | |
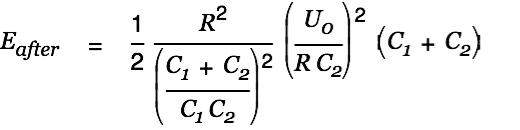 | |
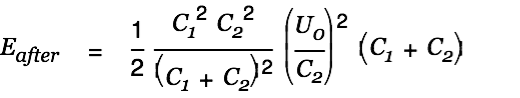 | |
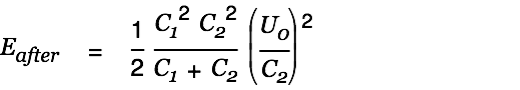 | |
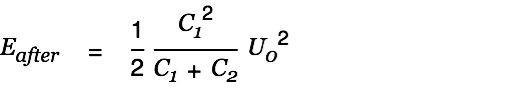 | |
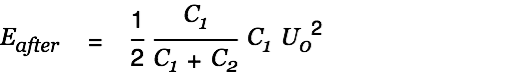 |
The difference between these two energies is the heat loss.
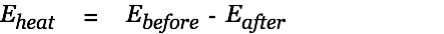 | |
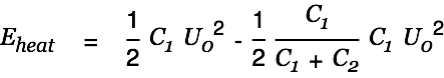 | |
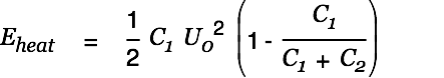 | |
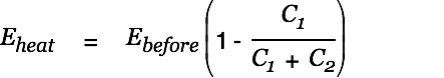 |
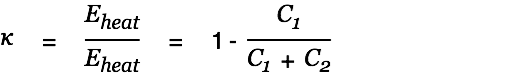 | (10) |
The goal was to pump energy from a small HV cap into a larger LV cap (energy reservoir). This means we have
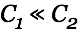 and thus
and thus 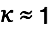 . Almost the entire energy is lost in the wire resistance as heat. For
. Almost the entire energy is lost in the wire resistance as heat. For 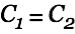 we have
we have 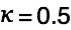 meaning that half the energy is lost. Note that
meaning that half the energy is lost. Note that 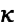 is independent of
is independent of 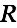 so using thick wire wouldn't help a bit.
so using thick wire wouldn't help a bit.
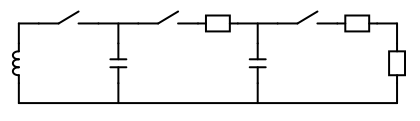
Energy transfer from one capacitor to another via a choke
We have shown in Energy transfer from ... that transfering energy from one cap to another by means of a wire with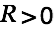 causes an unacceptable heat loss. For two identical caps half of the energy is lost. For a smaller source cap the outcome is even worse. It is therefore suggested to introduce a choke into the circuit as shown below.
causes an unacceptable heat loss. For two identical caps half of the energy is lost. For a smaller source cap the outcome is even worse. It is therefore suggested to introduce a choke into the circuit as shown below.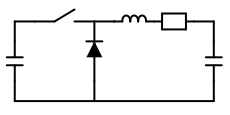 |
Once the source cap has reached a low enough potential the coil becomes an active component and converts its magnetic energy back into current and thus contributes to the filling of the target cap. The above circuit (switch closed) is described by the following differential equation.
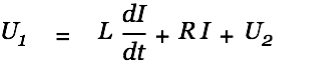 | |
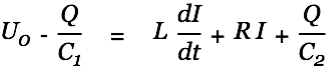 |
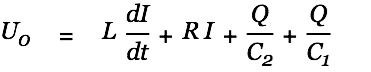 | |
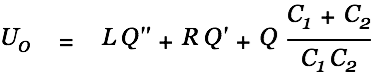 |
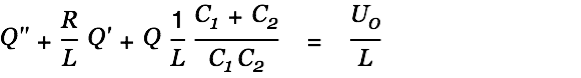 | (11) |
We solve the homogeneous differential equation
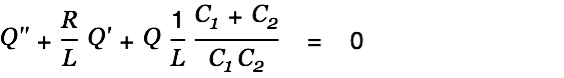 | (12) |
first using the following approach:
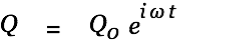 | |
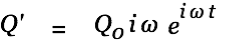 | |
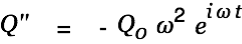 |
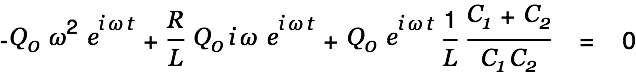 | |
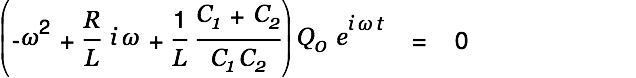 |
This equation is true for all
 if we have
if we have
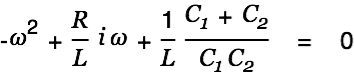 | |
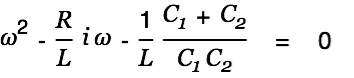 |
This equation is solved by
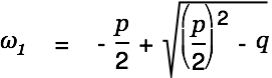 | |
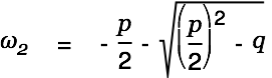 |
with
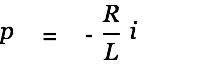 | |
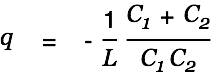 |
We consider
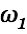 first.
first.
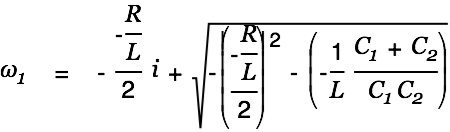 | |
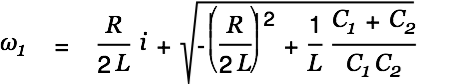 |
 | |
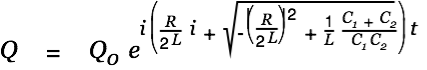 | |
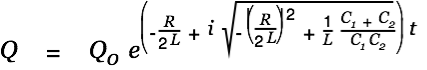 | |
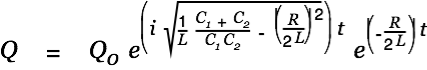 |
We can rewrite this as
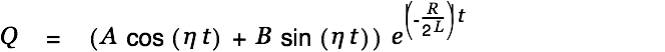 | (13) |
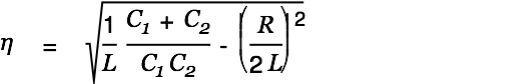 | (14) |
We solve the inhomogeneous differential equation by finding a particular solution
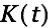 as follows:
as follows:
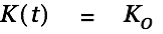 | |
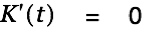 | |
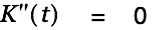 |
We substitute this as
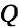 into Eq. 11.
into Eq. 11.
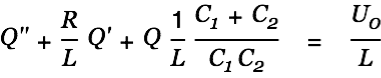 |
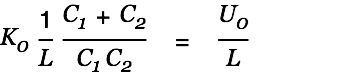 | |
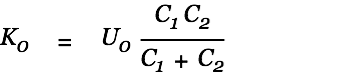 |
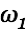 is then
is then
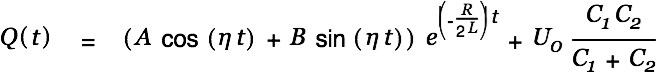 |
We demand
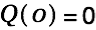 . This gets us
. This gets us
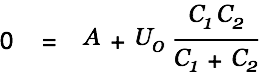 | |
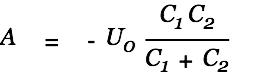 |
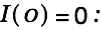
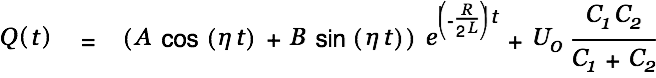 |
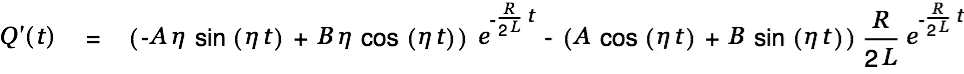 | |
 | |
 | |
 |
The special solution for our problem honoring our start conditions is therefore
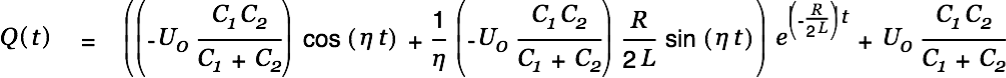 | |
 | |
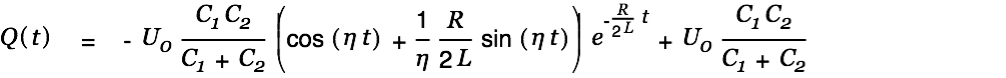 |
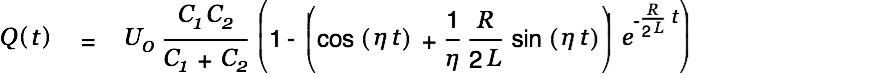 | (15) |
The voltage in the target cap is given by
 | |
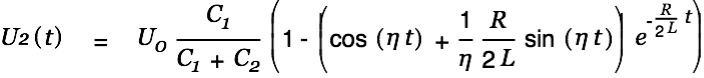 |
The current is given by
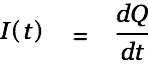 |
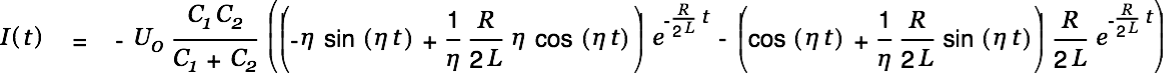 | |
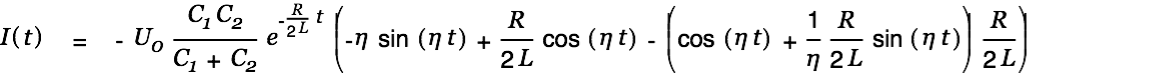 | |
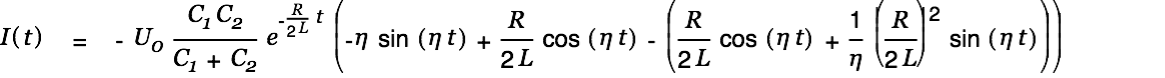 | |
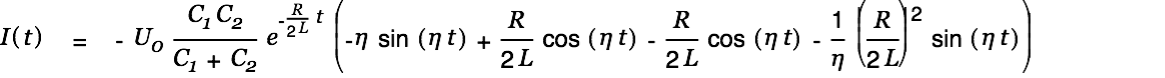 | |
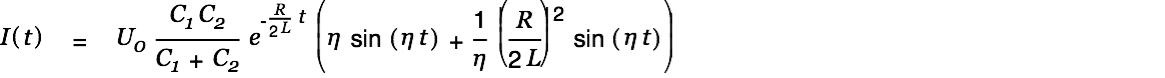 | |
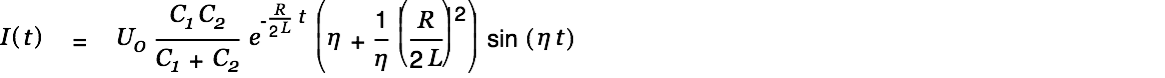 |
The voltage in the source cap is given by
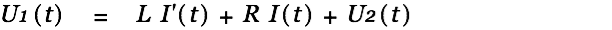 | (16) |
with
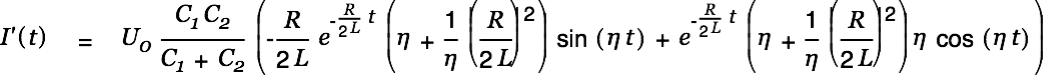 | |
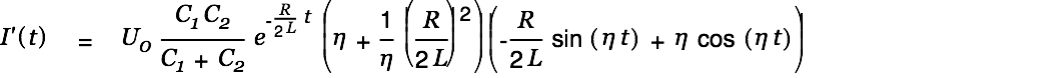 |
 |
The different outcome is obvious and this time highly dependent on the size of the wire resistance  .
.
Energy consideration
The energy in at
at 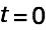 is given by
is given by
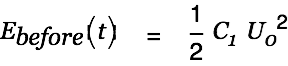 |
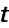 is given by
is given by
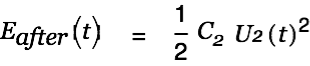 |
The following figure shows the development of
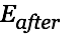 (energy in
(energy in 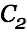 ) in relation to the initial input energy
) in relation to the initial input energy 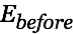 .
.
 |
There is a point with maximal current in the choke. The voltage potential between
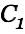 and
and 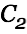 plus the voltage drop over
plus the voltage drop over 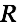 has dropped to zero and the choke starts to discharge its magentic energy into the target cap. The heat loss is minimal inspite of a significant wire resistance in this example. We create a new plot with more likely values for the components.
has dropped to zero and the choke starts to discharge its magentic energy into the target cap. The heat loss is minimal inspite of a significant wire resistance in this example. We create a new plot with more likely values for the components. |
Our circuit equations do not honor the diode that suppresses oscillations and prevents 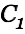 from being charged negatively. The energy of the coil would mainly go into
from being charged negatively. The energy of the coil would mainly go into 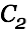 where it belongs with the diode in place. We can conclude that the choke approach transfers almost 100% of the energy in
where it belongs with the diode in place. We can conclude that the choke approach transfers almost 100% of the energy in 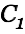 to
to 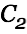 with no apparent heat loss. In a real application the inductivity should be chosen as small as possible to ensure fast enough energy transfer from left to right but large enough to prevent significant voltage drops over the wire.
with no apparent heat loss. In a real application the inductivity should be chosen as small as possible to ensure fast enough energy transfer from left to right but large enough to prevent significant voltage drops over the wire.
 |
 |
 |
Finding the optimal inductivity
We consider the inductivity to have the optimal value when the efficiency has a maximum. Handling this problem with a changing supply voltage in a bit complex. We therefore replace the energy source cap with a battery (constant voltag power supply). We then have
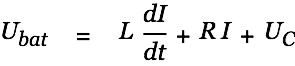 |
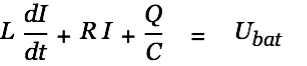 | |
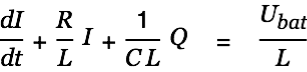 |
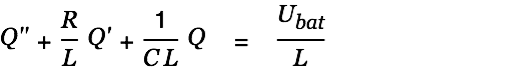 | (17) |
We again solve the homogenous equation first.
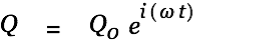 | |
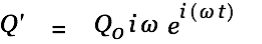 | |
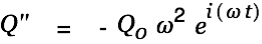 |
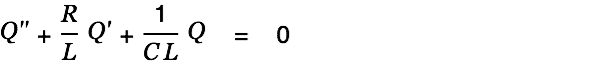 | |
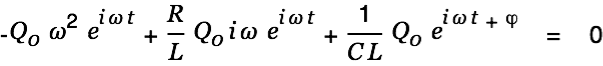 | |
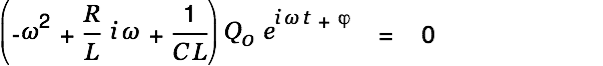 |
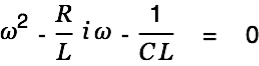 |
This equation is solved by
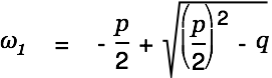 | |
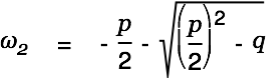 |
with
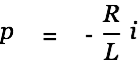 | |
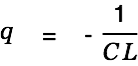 |
We consider 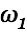 first.
first.
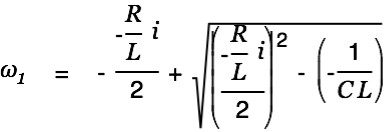 | |
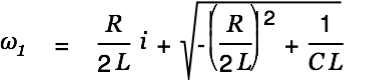 |
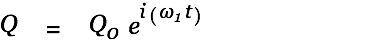 | |
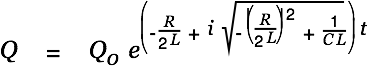 |
We solve the inhomogeneous differential equation by finding a particular solution 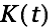 as follows:
as follows:
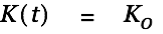 | |
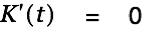 | |
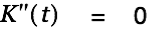 |
We substitute this as
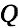 into Eq. 17.
into Eq. 17.
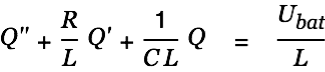 |
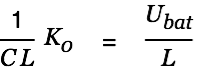 | |
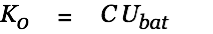 |
The complete general solution is then
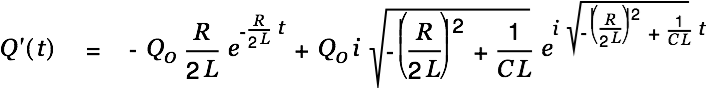 |
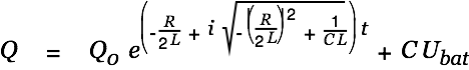 |
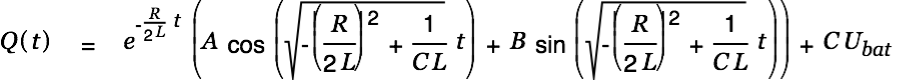 | |
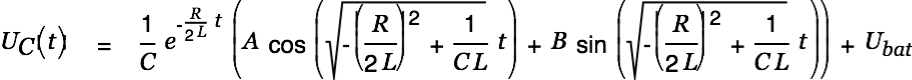 |
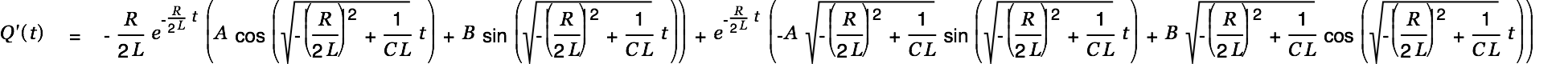 | |
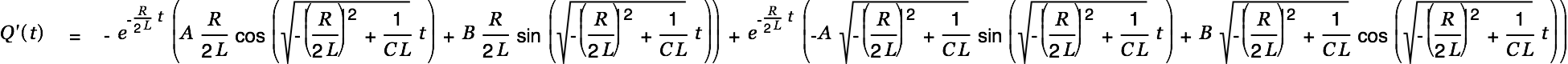 | |
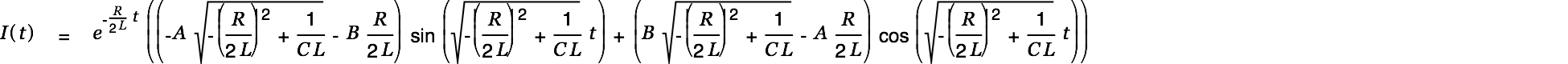 |
We assume
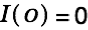 :
:
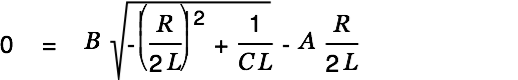 | |
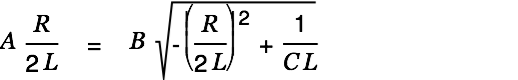 | (18) |
We assume
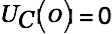 :
:
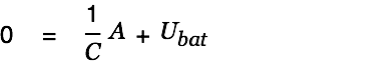 | |
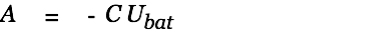 | (19) |
We substitute this into Eq. 18:
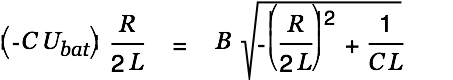 | |
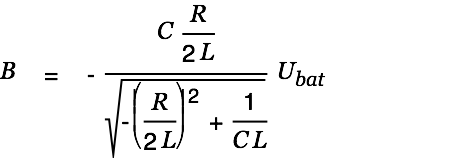 |
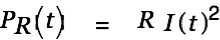 |
 |
News
| 23.04.2023 | Cassiopeia 2.9.0 released |
| 05.10.2022 | Cassiopeia 2.8.3 released |
| 29.09.2022 | Cassiopeia 2.8.0 released |
| 08.07.2022 | Cassiopeia 2.7.0 released |
| 14.04.2021 | Cassiopeia 2.6.5 released |
| 10.02.2021 | Cassiopeia 2.6.1 released |
| 26.06.2015 | Word Processor Comparison |
| 24.06.2015 | Updated Documentation |
| 23.06.2015 | Cassiopeia Yahoo Group |
| 18.06.2015 | Advanced Data Security |
| 11.05.2015 | Cassiopeia Overview |
| 08.05.2015 | Exporting to files |
| 14.05.2013 | LaTeX and HTML Generation |
| 08.05.2013 | Example Paper released |
| 26.04.2013 | Co-editing in a workgroup |
| 16.04.2013 | Equation Editor Quick Reference |
| 12.04.2013 | Equation Editor |
| 04.04.2013 | Links and Bibliography |
| 01.04.2013 | Books |
| 30.03.2013 | Documents |
| 28.03.2013 | Simulations |
| 16.03.2013 | 2D Graphs |
| 10.03.2013 | Symbolic Algebra |
| 08.03.2013 | Getting Started |
| 07.03.2013 | Installation and Setup |
White Papers
| 13.10.2015 | 01 Writing documents |
| 15.10.2015 | 02 Using the equation editor |
Youtube
| 08.07.2022 | Installation & Getting Started |
| 14.04.2021 | Animating Wave Functions |
| 26.01.2016 | Keystroke Navigation |
| 22.10.2015 | Equation Editor Demo |
| 19.06.2015 | Equation Editor Tutorial |
| 10.06.2015 | Sections and Equations |
| 09.06.2015 | Getting Started |
| 09.06.2015 | Damped Oscillations |
| 29.05.2015 | Solving equations |
| 13.05.2015 | Privileges and Links |
| 19.06.2013 | Magnetic Field |
| 14.06.2013 | Creating Documents |
| 10.06.2013 | Vector Algebra |
| 30.05.2013 | Differential Simulations |
Contact
Smartsoft GmbH Advanced Science Subdiv.Support: support@advanced-science.com

