Vector Potential
We have found the following set of equations to describe electromagnetic phenomena:
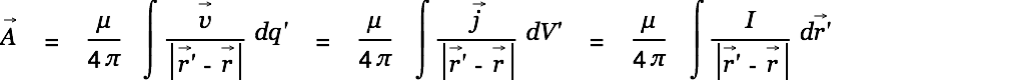 | (1) |
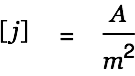 |
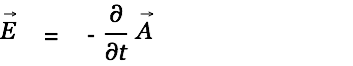 | (2) |
A current
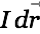 at some point
at some point 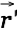 causes a vector potential
causes a vector potential 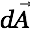 at a point
at a point 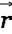 . A changing vector potential on the other hand causes an electromotive force on charges. The above equations are valid only if the permeablity is constant and homogeneous in the region of space we are looking at.
. A changing vector potential on the other hand causes an electromotive force on charges. The above equations are valid only if the permeablity is constant and homogeneous in the region of space we are looking at.
Current carrying straight conductor
We look at a short straight conductor of length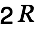 and determine the vector potential at distance
and determine the vector potential at distance 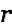 from the wire (at the center of the conductor).
from the wire (at the center of the conductor).
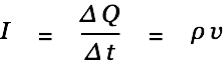 |
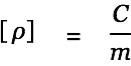 |
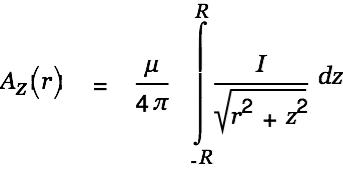 |
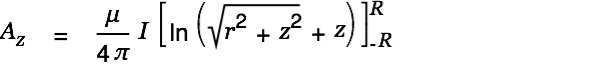 | |
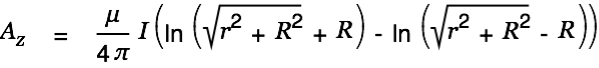 |
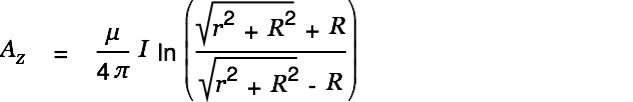 | |
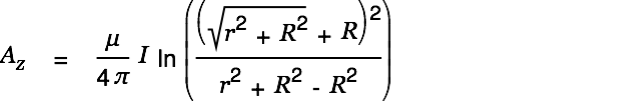 | |
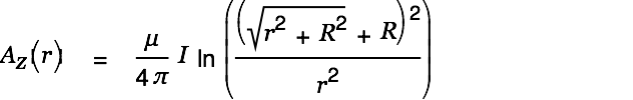 | (3) |
 |
This makes total sense. We have a rather high vector potential (aether wind) close to the conductor. The wind gets smaller with increasing distance from the wire.
We calculate the magnetic field  now. The rotation of a vector field in cylinder coordinates is given by
now. The rotation of a vector field in cylinder coordinates is given by
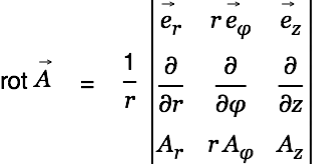 |
Since we have
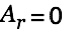 and
and 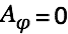 in our special case this simplifies to
in our special case this simplifies to
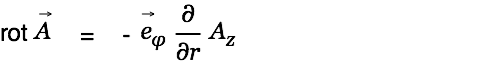 | |
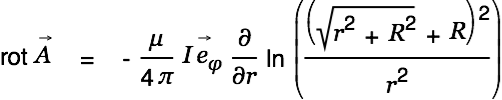 |
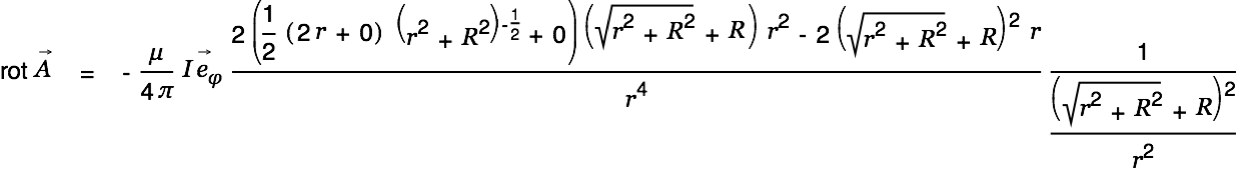 | |
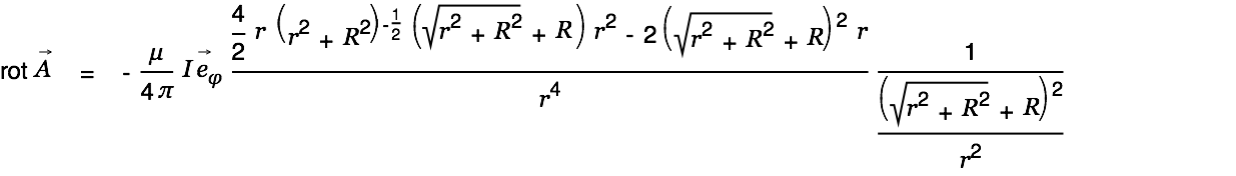 | |
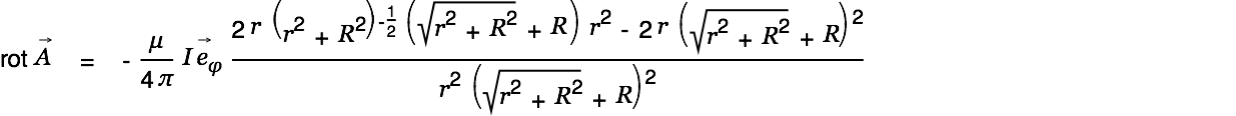 | |
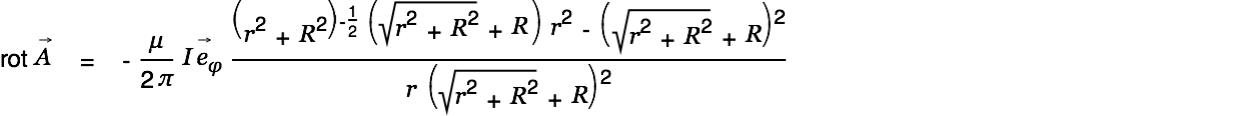 | |
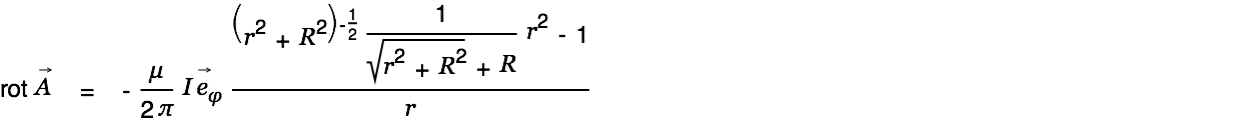 | |
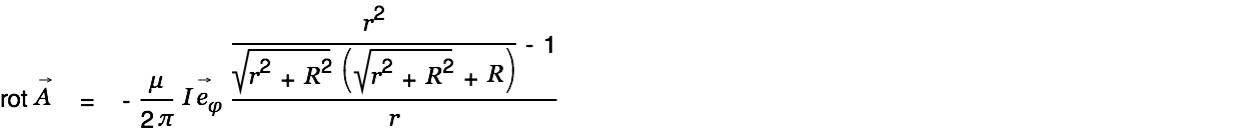 | |
 | |
 |
This gives us the magnetic field for the short wire:
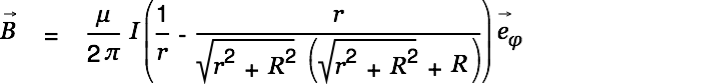 | (4) |
For
 we get
we get
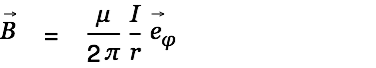 | (5) |
which is the accepted expression for a very long straight wire found in many text books.
Current carrying soleonoid
We try to determine the vector potential outside of a soleonoidal coil.
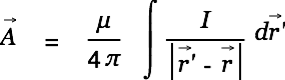 |
The integration path is given by
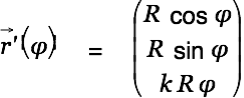 |
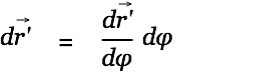 | |
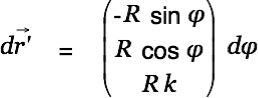 |
We look at a soleonoidal coil of length
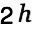 with its center in the origin of the coordinate system and
with its center in the origin of the coordinate system and
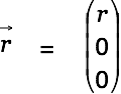 |
We then have
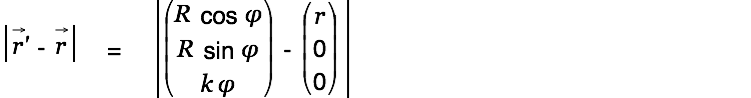 | |
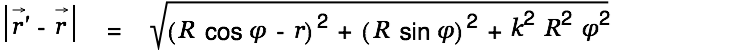 | |
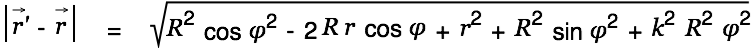 | |
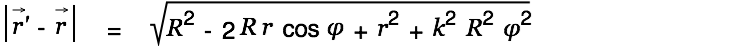 |
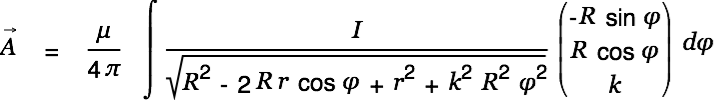 | |
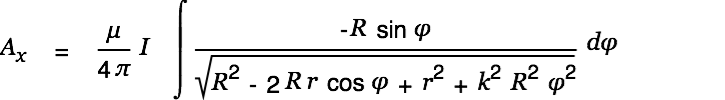 | |
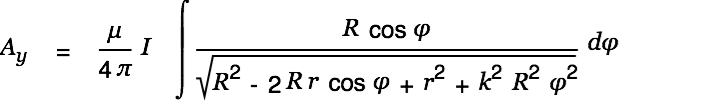 | |
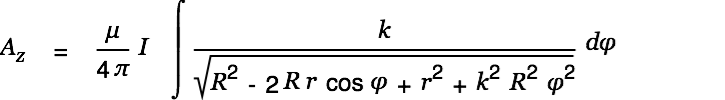 |
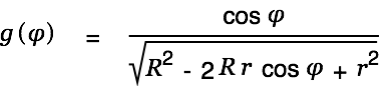 |
 |
Moving charges in the aether
Let's consider a charge moving with velocity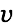 through the aether. We assume the majority of aether particles to be at rest. Very few are moving slowly towards a center of mass (far away) to feed its matter. This gives us a small and mainly constant vector potetial (aether wind)
through the aether. We assume the majority of aether particles to be at rest. Very few are moving slowly towards a center of mass (far away) to feed its matter. This gives us a small and mainly constant vector potetial (aether wind) 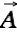 . The moving charge therefore experiences
. The moving charge therefore experiences 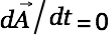 and thus no accelerating or decelerating force. The charge moves with (almost) constant velocity. We say almost because the behaviour of planets suggest that there is a minor friction component involved in celestial mechanics causing all orbits to eventually end up in circles. However, this friction is extremely weak.
and thus no accelerating or decelerating force. The charge moves with (almost) constant velocity. We say almost because the behaviour of planets suggest that there is a minor friction component involved in celestial mechanics causing all orbits to eventually end up in circles. However, this friction is extremely weak.Let's revisit our expression Eq. 3 for the vector potential caused by a current carrying straight conductor
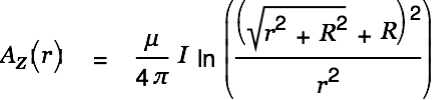 |
and assume that a test charge
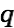 moves with velocity
moves with velocity 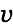 towards the center of the wire. The charge will experience an ever increasing vector potential (perpendicular to its movement). According to Eq. 2
towards the center of the wire. The charge will experience an ever increasing vector potential (perpendicular to its movement). According to Eq. 2
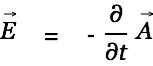 |
this should cause a force
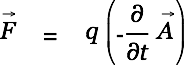 |
in accordance with conventional expectation (Lorentz Force).
A charge moving parallel to an (extremely long) current carrying wire would experience no change in 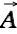 at the first glance and thus no force, at least not according to Eq. 1 and Eq. 2. However, another effect is to be looked at here. Let's consider two charges
at the first glance and thus no force, at least not according to Eq. 1 and Eq. 2. However, another effect is to be looked at here. Let's consider two charges 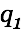 and
and 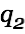 , each moving with velocity
, each moving with velocity
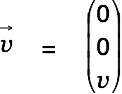 |
but displaced by
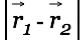 . Let's look at the scene at
. Let's look at the scene at 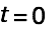 where
where
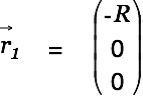 |
and
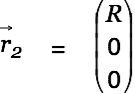 |
The vector potential along the x-axis is then
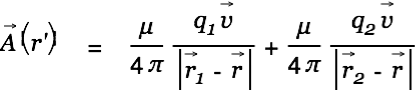 |
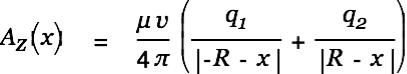 |
 |
It can clearly be seen that the vector potential is larger between the two moving charges, assuming that we can add up the vector potential caused by the two charges which seems reasonable. According to Bernoullie this higher velocity of aether causes a region of less pressure between the two charges which eventually leads to an additional aether wind component directed inwards.
To get a reasonable prediction for interaction of matter in space we have to marry
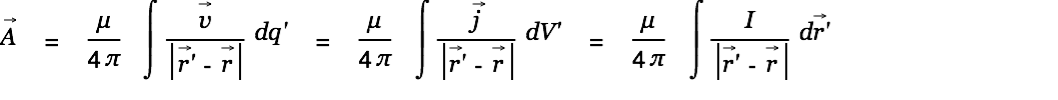 |
with
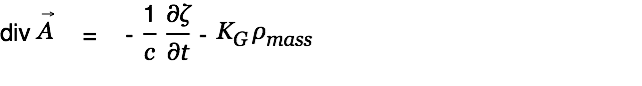 |
and
 |
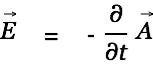 |
A r
What happens if we place a sheet of bismuth (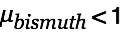 ) over a magnet? The magnet rotates the aether. Since aether velocity has to be continuous due to viscosity of the aether, the aether winds in the air on top of the magnet are extremely high. Above the air gap in the bismuth structure, the winds have to be ...
) over a magnet? The magnet rotates the aether. Since aether velocity has to be continuous due to viscosity of the aether, the aether winds in the air on top of the magnet are extremely high. Above the air gap in the bismuth structure, the winds have to be ...
New Aether Model
A current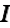 through a wire causes (with time retardation) a vector potential
through a wire causes (with time retardation) a vector potential 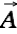 at some point
at some point 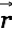 .
.
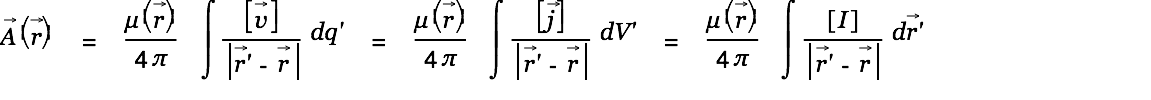 |
The square brackets in this equation is the retardation symbol indicating that the quantities between the brackets are to be evaluated for the time
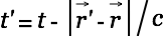 .
.
Let 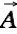 be a vector field on a bounded domain
be a vector field on a bounded domain 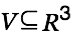 , which is twice continuously differentiable, and let S be the surface that encloses the domain V. Then
, which is twice continuously differentiable, and let S be the surface that encloses the domain V. Then 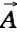 can be decomposed into a curl-free component
can be decomposed into a curl-free component 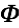 and a divergence-free component
and a divergence-free component 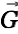 (Helmholtz's Theorem):
(Helmholtz's Theorem):
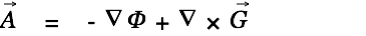 | |
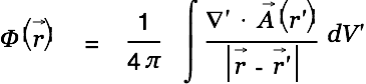 | |
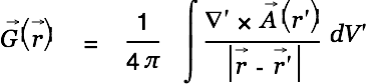 |
This allows us to write
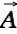 as
as
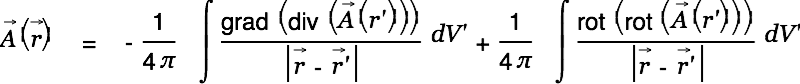 |
To simplify things let's (for now) assume that space is void of matter (no aether consumtion) and that the aether is not compressed (moderate current changes). We then have 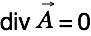 and can then simplify to
and can then simplify to
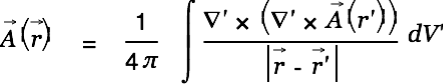 |
We make the educated guess that a changing vector potential generates an electromagnetic force.
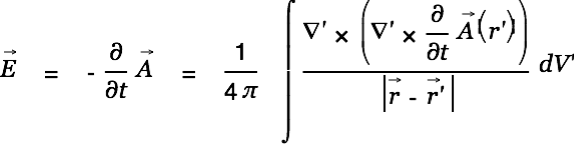 |
With the vector identity
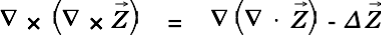 |
this can be rewritten to
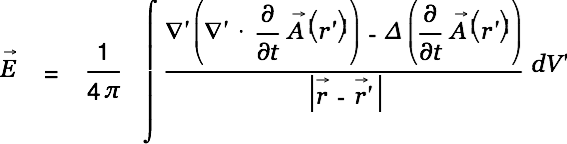 |
We (again) assume that
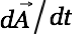 is divergence free and thus simplify to
is divergence free and thus simplify to
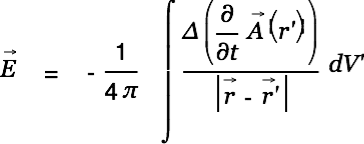 |
Jefimenko
Jefimenko reflects over Maxwells equations
 | (6) |
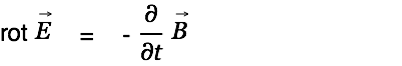 | (7) |
He uses the Helmholtz Theorem
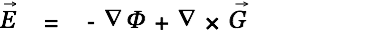 | |
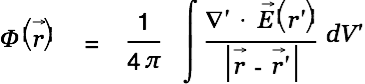 | |
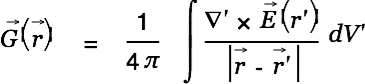 |
to write
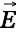 like so
like so
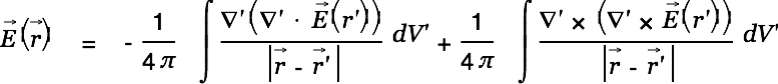 |
He then assumes charge free space 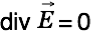 and therefore simplifies to
and therefore simplifies to
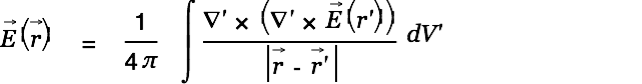 | (8) |
He then substtutes Eq. 7 into Eq. 8 and gets
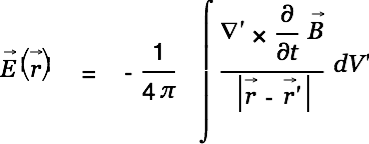 |
He now utitlizes the vector identity
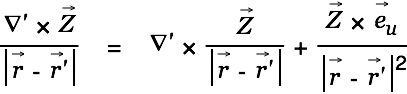 |
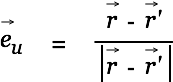 |
to get
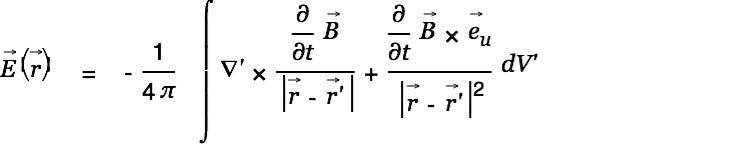 | (9) |
He uses another vector identity
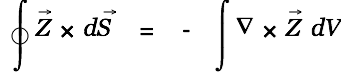 |
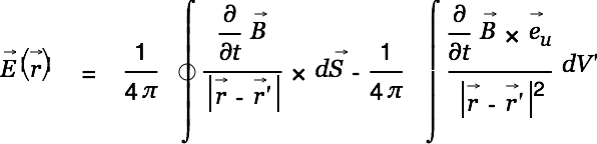 |
puts the surface
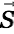 far far away (where
far far away (where 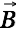 is zero) and thus simplifies to
is zero) and thus simplifies to
 |
News
| 23.04.2023 | Cassiopeia 2.9.0 released |
| 05.10.2022 | Cassiopeia 2.8.3 released |
| 29.09.2022 | Cassiopeia 2.8.0 released |
| 08.07.2022 | Cassiopeia 2.7.0 released |
| 14.04.2021 | Cassiopeia 2.6.5 released |
| 10.02.2021 | Cassiopeia 2.6.1 released |
| 26.06.2015 | Word Processor Comparison |
| 24.06.2015 | Updated Documentation |
| 23.06.2015 | Cassiopeia Yahoo Group |
| 18.06.2015 | Advanced Data Security |
| 11.05.2015 | Cassiopeia Overview |
| 08.05.2015 | Exporting to files |
| 14.05.2013 | LaTeX and HTML Generation |
| 08.05.2013 | Example Paper released |
| 26.04.2013 | Co-editing in a workgroup |
| 16.04.2013 | Equation Editor Quick Reference |
| 12.04.2013 | Equation Editor |
| 04.04.2013 | Links and Bibliography |
| 01.04.2013 | Books |
| 30.03.2013 | Documents |
| 28.03.2013 | Simulations |
| 16.03.2013 | 2D Graphs |
| 10.03.2013 | Symbolic Algebra |
| 08.03.2013 | Getting Started |
| 07.03.2013 | Installation and Setup |
White Papers
| 13.10.2015 | 01 Writing documents |
| 15.10.2015 | 02 Using the equation editor |
Youtube
| 08.07.2022 | Installation & Getting Started |
| 14.04.2021 | Animating Wave Functions |
| 26.01.2016 | Keystroke Navigation |
| 22.10.2015 | Equation Editor Demo |
| 19.06.2015 | Equation Editor Tutorial |
| 10.06.2015 | Sections and Equations |
| 09.06.2015 | Getting Started |
| 09.06.2015 | Damped Oscillations |
| 29.05.2015 | Solving equations |
| 13.05.2015 | Privileges and Links |
| 19.06.2013 | Magnetic Field |
| 14.06.2013 | Creating Documents |
| 10.06.2013 | Vector Algebra |
| 30.05.2013 | Differential Simulations |
Contact
Smartsoft GmbH Advanced Science Subdiv.Support: support@advanced-science.com

